Solid etalons, air spaced etalons, piezo tunable etalons, Gire Tournois etalons, LightMachinery has extensive expertise in the manufacturing and testing of all kinds of Fabry Perot etalons from 1mm square to 100mm in diameter.  These devices require high quality, very flat optical surfaces and extreme parallelism to achieve high performance, making them a good match for the polishing and metrology at LightMachinery.

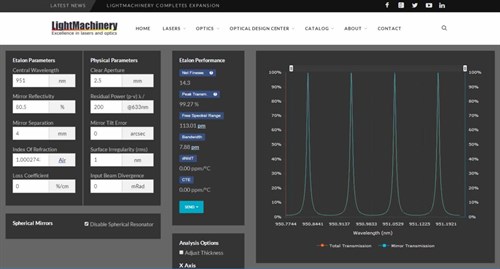
Etalons can be made from a wide variety of materials including; Fused Silica, Silicon and even Air.  Use our simple web based etalon calculator to determine the thickness and coating reflectivity to meet your requirements. 

Some Background on Fabry Perot Etalons

The Fabry Perot interferometer consists of two parallel flat semi-transparent mirrors separated by a fixed distance.  Light that enters the etalon undergoes multiple reflections and the interference of the light emerging from the etalon during each bounce causes a modulation in the transmitted and reflected beams.  During one return bounce the phase changes by 2πx2ndCOS(θ)/λ, where θ is the angle of the beam in the etalon.  Constructive and destructive interference occurs based on the angle of the beam (θ) the optical thickness of the etalon (nd) and the wavelength(λ).

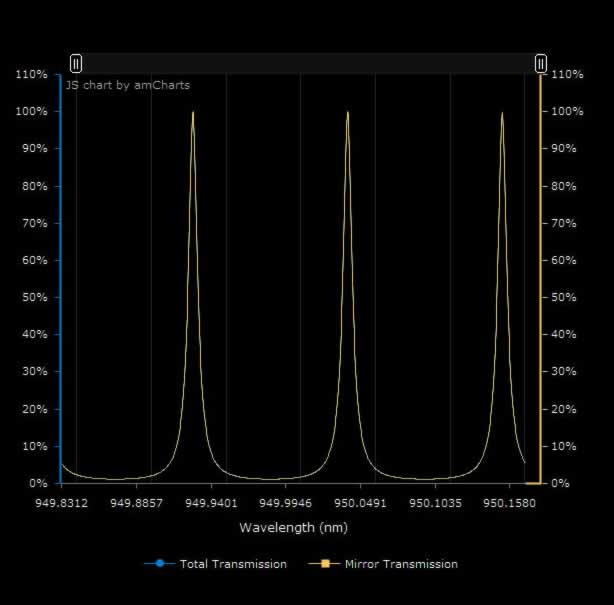
The transmission spectrum of an etalon will have a series of peaks, where constructive interference occurs, spaced by the 'free spectral range' or FSR.   As seen on the right in our online etalon designer.  If the absorption and scattering losses are small, the reflection spectrum of the etalon is 1 - T.

• FSR = 1/2nd cm-1   (wave number)
• FSR = λ²/2nd nm   (wavelength)
• FSR = c/2nd  Hz   (frequency)

You will notice that the mirror reflectivity is not part of these equations.  The mirror reflectivity does not affect the FSR, it affects the number of bounces and improves the quality of the modulation (more perfect bounces = better modulation).   As the reflectivity of the mirrors is increased the modulation peaks become sharper and decrease in width.  The full width at half maximum of the peaks is called the bandwidth and the ratio of the line width to the distance between the peaks (the FSR) is called the Finesse, F. So the Bandwidth = FSR / F.  And the finesse is the ratio of the FSR to the Bandwdth, F = FSR / Bandwidth.  

• Bandwidth is the full width at half maximum (FWHM) of the peak
• Bandwidth = FSR / F

The finesse is a dimensionless quantity and the units of the Bandwidth are the same as the FSR.  

Another quantity, The Coefficient of Finesse, \(F = 4\mathcal{R}/(1 - \mathcal{R})^2\), and the maximum reflectivity of the etalon is \(\mathcal{R}_{max} = 4\mathcal{R}/(1+\mathcal{R})^2\).   The Coefficient of Finesse and the finesse are related by the equation \(\mathcal{F}=\pi/(2\arcsin{(1/\sqrt{F})})\)  which can be approximated to \(\mathcal{F}=\pi\sqrt{F}/2\) or \(\mathcal{F} = \pi\sqrt{\mathcal{R}} / (1 - \mathcal{R})\).  

Actual versus Theoretical Performance

Etalons are usually described in terms of FSR and finesse. In many textbooks, the finesse is calculated using only the parameter R, reflectivity of the mirrors as in F=PI/SQRT(4R/(1-R)^2).   The etalon is assumed to have no losses, like scatter or imperfect surface flatness. This is like our physics class questions that started by assuming "a mass is sliding down a frictionless incline...".  So a perfect etalon with no losses or imperfections will always have a 100% peak transmission.  

Limits to Finesse

In reality there are other factors that 'limit' the transmission and finesse such as surface irregularity, parallelism, coating scatter. Each one makes a contribution to limiting the finesse and then all these contributions are combined to come up with the expected finesse and transmission. In our etalon calculator the graph displays both the perfect theoretical transmission and the expected transmission taking into account all the defects in a real etalon.

Surface Figure

Surface figure is the rms variation of surface away from flat.  Spherical error is excluded from the rms surface figure and is treated separately.  Surface figure is usually measured at the HeNe laser wavelength of 633nm and is expressed as fractions of this wavelength. The numbers that are included in the calculator are examples of practical values such as;. 633/20 = 30nm and a more difficult to achieve, 633/200 = 3nm.

Tilt or Wedge

End mirrors that are not parallel cause a change in the phase of the beam across the etalon. This results in reduced finesse since not all the beam is emerging 'in phase' creating a bright fringe or 'out of phase' creating a dark fringe. The result is a low contrast mixing of dark and bright fringes.

Spherical Error

The same is true of spherical error, the phase of the light varies over the surface of the etalon due to the curvature of the surfaces.  The errors caused by both Wedge and Sphere are predictable and can be calculated in specific ways which is why they are called out specifically in our calculations for expected performance.

Scatter and Material Losses

Scatter causes light to leak out of the etalon while materials will absorb light during each pass. These losses are usually insignificant if the proper coatings and materials are used unless the finesse is very high (above ~200).

Each of the parameters that effects the finesse also limits the finesse to some value. 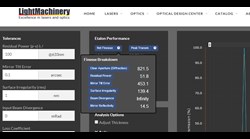A mirror reflectivity of 60% limits the finesse of an etalon to about 6.   In the same way all of the various defects each limits the finesse to some level and these limits can each be explored using our etalon calculator by hovering over the '?' on the finesse label as shown on the right.

Specifying Etalons

Etalons are generally specified by

• FSR
• Finesse
• Transmission
• Wavelength range
• Clear aperture

All of these specifications are measurable, functional specifications.  The reason that mirror reflectivity is not generally specified is that the reflectivity does not guarantee performance.  Scatter, surface errors and tilt can significantly reduce finesse and transmission below the finesse that would be expected from a given reflectivity.

Air Spaced versus Solid Etalons

Solid etalons are simple, flat, very parallel optical components. Sometimes these etalons are used uncoated using only the 4% fresnel refection to provide the etalon effect.  Uncoated etalons are often used inside laser cavities since only low finesse is required filter out unwanted laser wavelengths and uncoated etalons are very damage resistant.  But generally solid etalons are coated to increase the finesse of the etalon.  Both sides are coated with the same coating.   Solid etalons are often made from Fused Silica which is an extremely pure and homogeneous material.  Solid etalons are robust, simple devices however they are prone to two forms of temperature instability.  Both the index of the material and the physical thickness of the etalon material change with temperature.  In certain applications this temperature instability is unacceptable.  This temperature dependence can also be a useful method for tuning the transmission peak position of the since it effectively changes the thickness of the etalon.  This effect can be explored more fully in our etalon calculator.  

Air Spaced Etalons

Air spaced etalons reduce the temperature dependence problem by using air as the etalon medium, to greatly reduce the change in  refractive index with temperature.   The mirror spacing is now determined by spacers that may still be made from Fused Silica or by even more stable materials such as ULE or Zerodur.   Air spaced etalons are significantly more complex since there are now three components involved, two end mirrors and the spacer. The outside surfaces of the end mirrors also need to be wedged and AR coated to avoid reflections from these surfaces causing additional unwanted etalon effects.

Tunable Etalons

There are a number of ways to tune etalons including:  tilting the entire etalon, moving the mirrors and changing the index of the medium (pressure, temperature, electrostatic).  Tilt tuning is a simple tuning technique. As the etalon is tilted the FSR changes with the cosine of the angle.   Piezo electric tuning of an air spaced etalon is usually what is meant by the phrase "tunable etalon".  This technique can tune the etalon quickly by changing the size of the air gap.  By changing the length of the air gap by half the wavelength of the light, the transmission peak moves one full FSR.   So if an etalon is used at 532nm then only 266nm of motion is required to tune the etalon.  Small piezo elements can easily move through 10 microns.  Small tunable piezo etalons can be made by using a single hollow tube piezo stack, these are a standard item for us and have a clear aperture of about 4mm.  Larger piezo tunable etalons are made using 3 piezo elements.   Although these etalons are more complex to control they have the big advantage that the piezo elements can be subtly tuned to eliminate any residual tilt error between the two mirrors and improve the finesse.

VIPA Etalons

VIPAs are an interesting variant on the etalon.  They are simply an etalon with a built in transmission window so the beam can sneak in past the first reflector and effectively commence the multiple reflections and constructive and destructive interference from inside the etalon.  By changing the first reflector to a full 100% high reflector, the beam can only exit in transmission, this effectively creates an etalon with ~100% transmission.  But wait, isn't the point of an etalon to change transmission with wavelength.  Yes but.  Because the light is focussed into the entrance window of the VIPA, the transmission only occurs for specific angles that meet the constructive interference requirement.  What happens to the light at the wrong angles?  Surprisingly it just morphs into the right angles and transmits.  Learn more about VIPAs on our VIPA page or try the VIPA calculator.   

Questions?

We have tried to cover the basics of etalons but if you have any questions do not hesitate to contact us.

Symbols used in the equations

n = Index of refraction of the etalon medium
λ = central wavelength of interest
R = Reflectivity of each surface of the etalon (assumed to be the same)
d = thickness of the etalon
θ = angle of the beam inside the etalon
c= Speed of Light
F = Finesse
F = Coefficient of finesse

Recent work at LightMachinery

Stunning etalon fringe pattern, the ring pattern formed from the large angles of light from a UV black light. click to enlarge

The instrument also has a 70nm raised step over half the aperture, creating an offset fringe pattern. The piezo tuning is very smooth despite the load of the inch thick ultra-flat plates.

Not all of our etalons are large, here are some micro air spaced etalons made with zerodur for the ultimate in temperature stability

Silicon etalon spacer, hand-lapped inside and out, with a vent hole.

Solid silicon etalons, 25mm in diameter. The FSR of the etalons is 833MHz.

Two small (~30mm diameter) air spaced etalons with lambda/200 rms air gap uniformity.

LightMachinery is the leader in custom designed and manufactured VIPA etalons

A beautiful pair of matched solid etalons

A giant 60mm aperture piezo tunable Fizeau interferometer. End plates are matched to lambda/100 over the full aperture. This instrument uses the same method of 3 piezo stacks to allow the end mirror to be trimmed for perfect alignment and then the FSR can tuned or scanned through 9um's of movement.

A 10GHz air spaced etalon with 3 zerodur spacers optically contacted using epoxy free bonding. A very high finesse etalon with a 10mm clear aperture.

This is a 2mmx4mm micro solid etalon, held in plastic tweezers

1" diameter coated fused silica etalon with a finesse of 6 in the visible

1" diameter fused silica etalon with a finesse of 30 from 530nm to 660nm

Try the Etalon Designer in the LightMachinery Optical Design Center. It's fun, free and very useful

The emission lines of Mercury measured by Dillon Eaton and Mhlonishwa Mabuza for Professor Michael M. Kash of Lake Forest College. These lines were used to calibrate the etalon for measurement of the Sodium D lines.

Sodium D Lines measured as 593.0 +/- 4.5 nm, 591.1 +/- 5.0 nm with a difference of 0.604 +/- 0.025 (matching the accepted values of 589.5924 nm, 588.9951 with a difference of 0.5973 nm) . Also courtesy of Lake Forest College

The image shows the interference ring-splitting due to the Zeeman effect in mercury. The photons are from the 6D to 6P transition, and have a wavelength of 579.1 nm in the absence of a strong magnetic field. With the addition of a strong magnetic field, the splitting shows that mercury energy levels are quantized, and the emitted photons are shifted in wavelength in proportion to the strength of the applied magnetic field. Photo courtesy of Dr Bryce Bennett, Royal Military College, Kingston

A long air spaced etalon with a finesse of 3000 at 1064nm. The FSR is 880MHz and the bandwidth is less than 300KHz. A long zerodur spacer is used along with high reflectivity curved mirrors. The assembly is done using optical contacting.

Separation between hydrogen alpha (656 nm) for hydrogen and deuterium - Courtesy of the Observational Cosmology Lab at the NASA Goddard Space Flight Center

Hydrogen alpha (red) and hydrogen beta (486 nm). Both lines are split between hydrogen and deuterium - Courtesy of the Observational Cosmology Lab at the NASA Goddard Space Flight Center

A tunable Fabry Perot etalon uses piezo electric cylinders to adjust the size of the air gap and sweep the peaks of the etalon.

Transmission fringes from a Mercury 'black light' using a small piezo tunable etalon (OP-1986)

A fixed (non tunable) air spaced etalon for use in the visible with a 20um air gap

Up close with the 20 um fixed air gap etalon looking at a black light

Check out our Catalog and our Calculators!

Optics Catalog

Most of the optics we make are custom made but we still have an interesting catalog.  Check it out! 

Optical Design Center

Design etalons, lenses, resonators, VIPA's and explore optical material properties.